Tuenti Challenge 7
Cuando queremos aprender un nuevo lenguaje o paradigma, sólo nos queda practicar para asimilarlo. Es por esto que me gusta realizar problemas y retos no sólo para perfeccionar mi dominio de Clojure, si no también para descubrir y aprender nuevos enfoques a la hora de afrontar los problemas.
La semana pasada terminó la séptima edición del Tuenti Challenge. Una colección de problemas de programación, análisis, optimización y hacking para los amantes de los retos. Podéis consultar los 15 problemas de los que constó esta edición en la página del concurso.
Aquí os dejo el análisis de los problemas y estrategia que implementé de los problemas que pude hacer y el código de las soluciones.
- 1. Pizza love
- 2. Bowling
- 3. Board games
- 4. Help Pythagoras Junior
- 5. Ghost in the HTTP
- 6. The Tower
- 7. Word Soup Challenge
- 8. Uni code to rule them all
- 9. The Supreme Scalextric Architect
- 10. Passwords
- 11. Colors
- 12. That’s a lot of moneyz
- 13. R’lyeh
1. Pizza love
El primer ejercicio suele ser sencillo, destinado principalmente a familiarizarse con el procedimiento de probar, enviar la fase de test y de submit, y tratar con los ejemplos difíciles que suelen desbordar los tipos de datos mas simples.
En este caso, nos dan una lista de número que representan el número de porciones que come cada persona. Sabiendo que las pizzas traen 8 porciones nuestro objetivo es averiguar cuantas pizzas necesitaremos comprar. Tan solo debemos sumar las porciones de todas las personas, dividir por 8 y redondear al siguiente entero Math.ceil.
(Math/ceil (/ slices 8))
2. Bowling
En esta ocasión tenemos que implementar el sistema de puntuación de los bolos. Las partidas constan de 10 rondas y en cada ronda tendremos que intentar tirar los 10 bolos y dos lanzamientos para conseguirlo. Si lo conseguimos a la primera habremos conseguido un “pleno” o “strike”. Si conseguimos tirar todos a la segunda será un “semipleno” o “spare”. Los puntos en cada ronda es igual al número de bolos tirados. Además si hicimos pleno o semipleno, sumaremos a la puntuación de ese ronda los bolos de las siguientes tiradas: los puntos de la siguiente tirada si hicimos semipleno y los puntos de las 2 siguientes tiradas si hicimos pleno.
Lo que tenemos es una secuencia con los bolos tirados y deberemos mostrar la puntuación obtenida en cada ronda. Hay que tener en cuenta que cada ronda puede constar de una tirada (si hacemos pleno) o de dos, por lo que deberemos ir llevando la cuenta para saber en que ronda nos encontramos. Además deberemos saber cuando se ha hecho pleno y semipleno para sumar puntos extras.
En el peor de los casos, si hacemos 3 plenos seguidos, estaríamos modificando el marcador de 3 rondas: la actual y las dos anteriores para contabilizar los puntos extras.
Podríamos ir leyendo tirada a tirada, y actualizando varios indicadores que nos digan si hicimos pleno o semipleno en las dos anteriores rondas. Pero ya que tenemos la secuencia completa de tiradas, es mas sencillo sumar directamente las tiradas futuras.
(defn bowling-score [rolls]
(loop [[score & _ :as scores] '(0)
[r1 r2 r3 & _ :as rolls] rolls]
(cond
(= 11 (count scores)) (-> scores reverse next)
(= 10 r1) (recur (conj scores (+ score r1 r2 r3)) (next rolls))
(= 10 (+ r1 r2)) (recur (conj scores (+ score r1 r2 r3)) (nnext rolls))
:else (recur (conj scores (+ score r1 r2)) (nnext rolls)))))
3. Board games
Ahora nos metemos en el papel de un diseñador de juegos de mesa. Nuestro objetivo es decidir cuántas cartas de puntos y de que cuantías necesitamos, para que combinándolas podamos conseguir todos las posibles puntuaciones que se pudieran dar en el juego. Por ejemplo, si nos dicen que un determinado juego de mesa se puede conseguir hasta 20 puntos, deberemos poder combinar nuestras cartas de puntos para poder obtener los valores del 1 al 20.
A priori pareciera que tuviéramos que generar combinaciones de cartas, y probar distintas opciones hasta obtener el mínimo número de cartas necesaria. Este es un problema mucho mas sencillo de lo que aparenta la descripción. Como las cartas no se pueden repetir, vemos que para cada determinada cuantía de puntos habrá cartas que estarán y otras que no estarán. Después de algunas pruebas veremos que el sistema que estamos buscando no es mas que la representación binaria.
Así que el problema se reduce a contestar, cuantos bits se necesitan para representar cada determinado número, que no es mas que el redondeo hacia arriba del logaritmo en base dos del número máximo.
Para un juego donde máximo puedes obtener 22 puntos necesitaríamos: ⌈ log₂ 22 ⌉ = 5. Por lo que necesitaríamos 5 bits, o lo que es lo mismo, 5 cartas con las potencias de dos: 1 2 4 8 16. En Java tenemos el logaritmo neperiano y en base 10, pero aplicando propiedades podemos obtener el valor dividiendo por el logaritmo de la base que queremos, en nuestro caso:
(Math/ceil (/ (Math/log 22) (Math/log 2)))
Otra opción sin usar logaritmos es ir multiplicando por dos tantas repetidamente hasta que lleguemos o nos pasemos del número objetivo. El número de veces que hemos multiplicado por dos será el número de cartas que necesitemos.
4. Help Pythagoras Junior
Tenemos que ayudar al nieto de Pitágoras a buscar el triangulo con menor perímetros entre todos los triángulos que se puedan formar dada una lista de posibles lados. Los triángulos pueden ser de cualquier tipo (no tienen porqué ser triángulos rectángulos como en el teorema de su abuelo), por lo que para formar un triángulo, la suma de los dos lados mas pequeños debe ser mayor que el lado mas grande. Podríamos probar por fuerza bruta todas las posibles combinaciones de los tres lados, comprobar que formen un triángulo, calcular su perímetro y buscar el mínimo de todos estos valores.
Aunque hallaríamos la solución, el problema sería computacionalmente inviable ya que el número de operaciones crecería exponencialmente. Debemos optimizar el algoritmo para que se pueda resolver en un tiempo razonable. Lo primero que haremos es ordenar todos los lados de menor a mayor y comenzaremos a probar. El algoritmo consiste en tres bucles anidados que calculan las combinaciones.
En el momento que encontramos un triángulo (a, b, c) sabemos que este triángulo será el menor de todos los posibles que tengan los lados a y b, ya que el resto de los lados serán mayor que nuestro cmin. Esta es una de las podas u optimizaciones que realizaremos.
a + b + c = x
a + b + c' = x'
si c' > c => x' > x
Junto con el valor del perímetro mínimo deberemos guardar también el valor de cmin. En el momento que b sobrepase al cmin del triangulo mínimo, todos los perímetros también serán mayores, por lo que debemos probar con el siguiente a.
a + b + c = x
a' + b' + c' = x'
a' > a, b' > c => x' > x
5. Ghost in the HTTP
Esta es una prueba de investigación. Sólo se nos presenta un enlace que al cargarlo, nos muestra un una página html simple con un mensaje y un nuevo enlace:
<a href="/ghost">Just a whisper. I hear it in my ghost...</a>
También podemos ver que que en el favicon aparece la palabra PUSH que será una pista para resolverlo. Si accedemos al enlace lo único que obtenemos es el texto:
iVBORw0KGgoAA
Que parece corresponder con datos con codificación base64. Si decodificamos estos datos vemos que parece la cabecera de una imagen PNG, pero el fichero es demasiado pequeño y no está completo.
echo "iVBORw0KGgoAA" | base64 -d | xxd
base64: invalid input
00000000: 8950 4e47 0d0a 1a0a 00 .PNG.....
Usando como pista el nombre del problema, echaremos un vistazo a las cabeceras HTTP de la petición:
$ curl -v -k https://52.49.91.111:8443/ghost
> GET /ghost HTTP/1.1
> Host: 52.49.91.111:8443
> User-Agent: curl/7.52.1
> Accept: */*
>
< HTTP/2 200
< accept-ranges: bytes
< content-type: text/plain; charset=utf-8
< last-modified: Mon, 24 Apr 2017 11:13:13 GMT
< content-length: 3445
< date: Fri, 05 May 2017 06:35:35 GMT
<
curl: (18) transfer closed with 3432 bytes remaining to read
iVBORw0KGgoAA
Aquí podemos ver por un lado, como el comando curl nos informa de que se ha cerrado la conexión. Vemos que la cabecera Content-Length nos informa que el recurso ocupa 3445 bytes pero el servidor sólo nos ha enviado 13 bytes. Revisando las cabeceras vemos que el servidor acepta rangos Accept-Ranges: bytes. Si probamos a curl a pedir un rango:
$ curl -v -k https://52.49.91.111:8443/ghost -r 13-
AANSUhEUgAAAN
Nos devuelve los siguientes 13 bytes del fichero!. Así que lo que tenemos que hacer es seguir haciendo peticiones en bloques de 13 bytes hasta obtener el fichero competo:
for r in $(seq 0 13 3445); do \
curl -v -k https://52.49.91.111:8443/ghost -r 13- >> ghost.b64 \
done
Una vez descargado y decodificado con base64 vemos que se trata de una imagen con el número 4017-8120 que parece ser un rango … Si probamos a pedir este rango concreto al servidor obtenemos la siguiente respuesta:
$ curl -v -k https://52.49.91.111:8443/ghost -r 4017-8120
> GET /ghost HTTP/1.1
> Host: 52.49.91.111:8443
> Range: bytes=4017-8120
> User-Agent: curl/7.52.1
> Accept: */*
>
< HTTP/2 200
< content-type: text/plain; charset=utf-8
< content-length: 48
< date: Fri, 05 May 2017 06:45:12 GMT
<
You found me. Pushing my token, did you get it?
Otra vez referencia a la palabra “push”. Podemos percatarnos que el servidor nos informa que soporta HTTP/2. Una de las nuevas funcionalidades de HTTP/2 es Server Push, que es la posibilidad de que el servidor envíe recursos antes que el cliente los solicite. Esto se hace para acelerar la carga de páginas, ya que con una única petición a un html, el servidor podría devolvernos el html solicitado junto las imágenes y el css que probablemente se vayan a pedir posteriormente.
El comando curl no soporta push, así que probamos con otro cliente que soporte HTTP/2 Server Push, y esta vez si vemos que el servidor nos había enviado (por push) la clave que estábamos buscando:
$ nghttp https://52.49.91.111:8443/ghost -H "Range: bytes=4017-8120"
YourEffortToRemainWhatYouAreIsWhatLimitsYou
You found me. Pushing my token, did you get it?
6. The Tower
Este problema parece estar inspirado la serie Tower of God. Nuestro objetivo es subir a lo alto de una torre de N plantas. Si estamos en la planta x, subir la escalera a la siguiente planta nos llevará x años. Bajar a la planta anterior no tiene coste. También nos informan de una serie de atajos entre plantas (que pueden subir o bajar). Nos piden averiguar el mínimo número de años que tardaríamos en llegar a lo alto de la torre.
Rápidamente se intuye que es un problema de grafos, donde cada planta puede ser un nodo, y los atajos y escaleras serán las aristas que tendrán distintos pesos en años. Así pues, tan solo deberemos aplicar el algoritmo de Dijkstra que nos averigüe el camino mas corto. Pero como siempre no suele ser tan sencillo. Generar un nodo por cada planta puede servir para los ejemplos simples, pero cuando nos encontramos con torres que tienen 10000 plantas, los tiempos se disparan.
Si analizamos el problema vemos que podemos simplificar el grafo. Un grafo con 100 nodos que se corresponda al camino de la planta 1 a la planta 100, sería equivalente a un grafo con 2 nodos, cuya arista cueste lo mismo que el sumatorio de todas las anteriores.
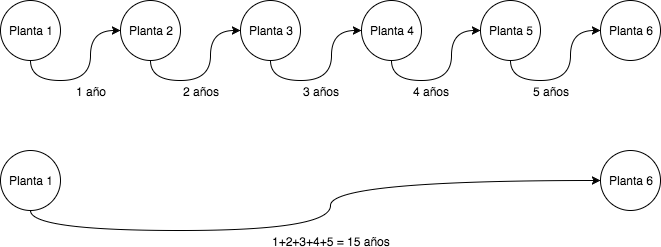
Por lo para la solución final formaremos un grafo que estará formado únicamente por los nodos que pertenezcan a atajos (además de la primera y última planta). A estos nodos agregamos las arista que corresponden a los atajos. Las aristas de coste cero cuando vamos hacia atrás, y calculamos las aristas que corresponderían al camino normal de subir las escaleras.
7. Word Soup Challenge
Si accedemos al enlace nos aparece el juego de sopa de letras. En este nivel tenemos 5 minutos para resolverlo. Si lo hacemos manualmente se nos mostrará el siguiente nivel que es una monstruosidad que ha de resolverse en 20 segundos.

Existen solucionadores de sopa de letras en javascript, por lo que parece que es tan simple como simular los clicks del ratón y listo. Pero como siempre, resulta que no es tan sencillo. Si vemos el código fuente vemos que el código JavaScript se carga dinámicamente a través de una conexión websocket. Además, los distintos intentos de hacer click desde javascript son infructuosos.
Usando las developer tools de chrome podemos poner un breakpoint global sobre los eventos de ratón. Al hacer click sobre una letra, podremos ver el código javascript que se ejecuta. Ahí podemos ver que se sobre escribe la variable $ y que se comprueba que el evento del ratón tenga activada la opción isTrusted que indica que es un evento de ratón real, motivo por el cual no podemos simularla con javascript.
Después de analizar un poco el código vemos que podemos comunicarnos directamente con el websocket utilizando estas dos funciones:
m = t => {
let n, e, o, s = 0;
const c = t + "-saltbae";
if (!c.length) return s;
for (n = 0, o = c.length; n < o; n++) e = c.charCodeAt(n), s = (s << 5) - s + e, s |= 0;
return Math.abs(s)
}
mark = (f, t) => {
e = `${f}-${t}`;
w.send(btoa(`${e}-${m(e)}`))
}
Por lo que sólo nos queda cargar jQuery, Wordfind, buscar la lista de palabras, el array bidimensional con las letras y solucionarlo:
solve = function () {
var words = jQuery("div[id^=word-]").toArray().map(function(e){ return e.innerText})
var board = jQuery("tr").toArray().map(e => jQuery("td", e).toArray().map(e => e.innerText))
wordfind.solve(board, words).found.forEach(mark)
}
8. Uni code to rule them all
Aquí ponen a prueba nuestra conocimiento sobre Unicode. El problema es tan sencillo como detectar en qué filas aparece un número, ignorando posibles espacios en blanco delante y detrás de este. Una vez detectado el número hay que mostrarlo en hexadecimal.
Puede que los ejemplos parezcan confusos al principio, hasta que caemos en la cuenta que los dígitos se pueden representar de distinta forma en otros idiomas!. Por ejemplo, esto es un teclado árabe donde se puede apreciar los grafos correspondientes a las letras y números occidentales:

Ya en el propio enunciado te indican que los números pueden estar representados en distintos idiomas. Unicode también agrupa los símbolos por categorias, concretamente tenemos que ver las dos que ya nos dicen en el enunciado, la Nd y la Zs.
Afortunadamente Java tiene soporte para Unicode, y lo que es aún mejor, las propias expresiones regulares soportan categorías de Unicode. Así que una expresión regular típica que busca dígitos ignorando los espacios que sería:
\s*\d+\s*
extendiendo esta expresión regular a las categorías Unicode sería:
\p{Zs}*\p{Nd}+\p{Zs}*
Tan solo debemos leer el fichero adecuadamente. Analizando los ficheros de prueba averiguamos que están en UTF-16 Little-endian, y que al principio del fichero tenemos dos bytes que forman el BOM (Byte Order Mark), bytes que nos informan que codificación se está utilizando. Como nosotros ya estamos forzando a que sea UTF-16LE podemos ignorar estos bytes.
Por último y como viene siendo habitual, hay que utilizar BigInteger para poder tratar con los números gigantes que vienen en las pruebas, además de que esta clase soporta la conversión de cadena Unicode a número, y la transformación de número a hexadecimal.
9. The Supreme Scalextric Architect
Este ha sido uno de mis favoritos. Dado un conjunto de piezas (secciones simples, dobles y curvas), nuestra misión es averiguar las piezas necesarias para construir el circuito mas grande posible. A priori el problema parece muy complejo ya que el número de combinaciones posibles parece bastante grande.
Pero pensamos en primer lugar en el circuito cerrado mas pequeño posible, nos daremos cuenta que es el compuesto por 4 curvas formando un círculo. De esto sabemos que si en el conjunto de piezas, no hay al menos 4 curvas, es imposible hacer un circuito cerrado.
Una vez tenemos el circuito mas pequeño podemos pensar en como agrandarlo. Vemos claramente que no se pueden agregar piezas individuales, si no que cada operaciones de crecimiento del circuito consiste en agregar un conjunto de piezas.
Por ejemplo, una transformación sería agregar dos piezas simples. Nos da igual si hacemos crecer el circuito a lo alto o a lo largo, porque al fin y al cabo estamos hablando del mismo circuito. Intentar agregar 10 piezas simples, sería como aplicar 5 veces esta transformación simple.
Si representamos cada operaciones como un vector de tres valores [S C D], con el número de piezas simples (S), curvas (C) y dobles (D), la transformación anterior se puede representar como [2 0 0]. Si analizamos las posibles mínimas transformaciones que podemos hacer nos encontraremos con las siguientes 12 transformaciones:
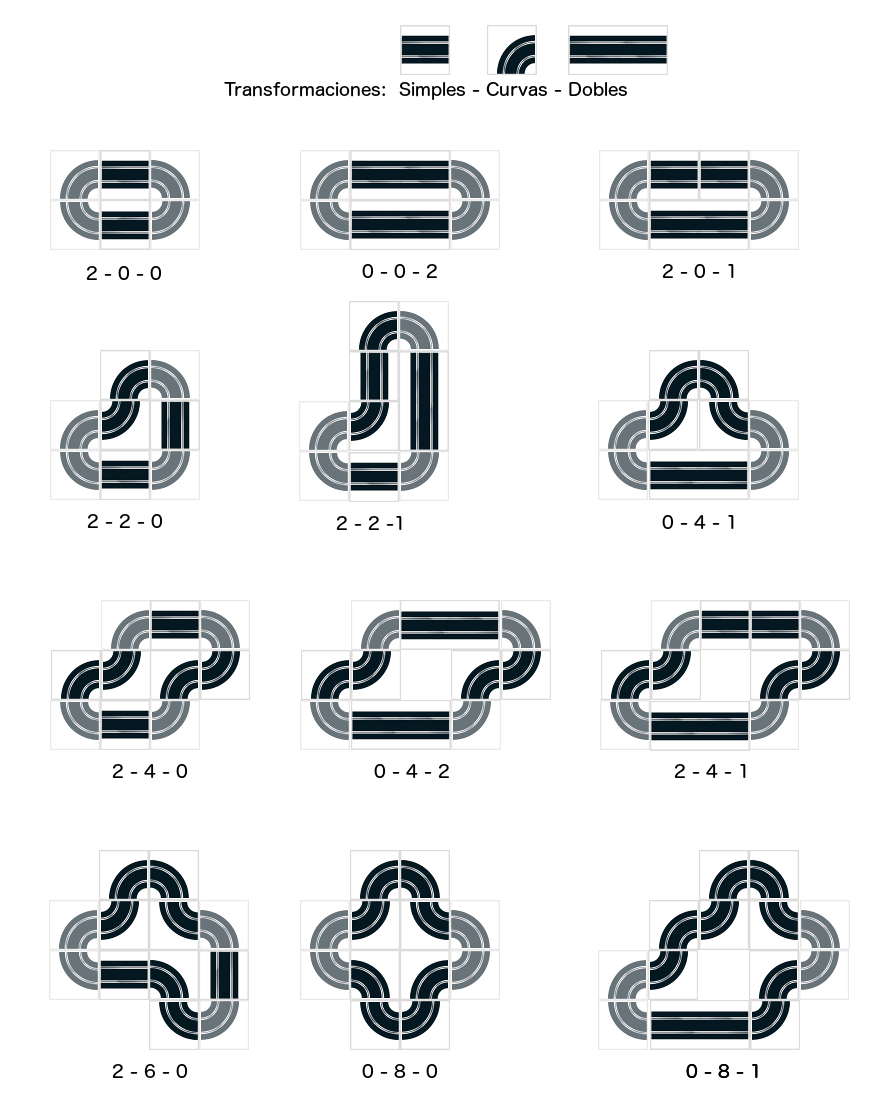
Cualquier otro circuito o transformación estaría compuesto por varias de estas 12 transformaciones mínimas. Ahora el espacio de búsqueda se reduce en gran medida y podemos abarcarla en tiempo. Empezaríamos con un vector que se corresponde con el número total de piezas disponibles, y comenzaríamos a aplicar transformaciones básicas que consistiría en restar el vector correspondiente. Además, dado un conjunto de piezas muy grande, podríamos simplificarlo eliminando de forma repetitiva un conjunto fijo de transformaciones como [8 8 8] por ejemplo.
10. Passwords
Hemos borrado la base de datos de contraseñas de los usuarios y debemos intentar restaurar los contraseñas de todos ellos. Afortunadamente las contraseñas son autogeneradas por un algoritmo que cambia cada día y tenemos el log de cuando cada usuario regeneró la contraseña. Como disponemos del repositorio git con el código del algoritmo, sólo tenemos que saber la fecha, buscar la versión del algoritmo y ejecutarlo. Para buscar la versión del código podemos utilizar el siguiente comando:
git rev-list -n 1 --before="FECHA" --all
Que quiere decir, busca la primera revisión (-n 1) anterior a la fecha dada, en todas las ramas (--all). Una vez tengamos el hash de la revisión solo debemos hacer checkout. Por ejemplo, veamos el tercer ejemplo:
xoajoj 2
2013-05-19 1
2016-08-20 1
Esto quiere decir que el usuario ‘xoajoj’ regeneró la contraseña en dos días distintos. Y en cada uno de estos día sólo se regeneró una sola vez. Para restaurar la contraseña haríamos lo siguiente:
$ git checkout $(git rev-list -n 1 --before="2013-05-19 23:59:59" --all)
Previous HEAD position was c4f77fc... Updating script
HEAD is now at 6ffca36... Updating script
$ ./script.php xoajoj
$t0\&wArw^ 08f654824c4c1144fc0fad332112d619
$ git checkout (git rev-list -n 1 --before="2016-08-20 23:59:59" --all)
Previous HEAD position was 6ffca36... Updating script
HEAD is now at c4f77fc... Updating script
$ ./script.php xoajoj 08f654824c4c1144fc0fad332112d619
WSUmXS~*oR 60c9c0f66b325c193d293ced8c85cf71
Con un poco de scripting podemos automatizar este proceso, pero pronto nos daremos cuenta de uno de los problemas. Y es que git rev-list realiza una búsqueda de los commits que están conectados por así decirlo. De modo que los commits que fueron eliminados o abandonados no aparecen. Pero a menos que hagamos un git prune, esos commits siguen estando en la base de datos, aunque no seamos capaces de llegar a ellos.
Después de varias pruebas, para solventar esto, me decidí a listar todos los objetos dentro de la base de datos .git/object. Para cada uno de ellos comprueba con git cat-file -t si son de tipo commit, y si lo son extraigo la fecha y el algoritmo con git show:
find .git/objects/ \
| egrep '[0-9a-f]{38}' \
| perl -pe 's:^.*([0-9a-f][0-9a-f])/([0-9a-f]{38}):\1\2:' \
| \
while read hash ; do
if [ "$(git cat-file -t $hash)" == "commit" ]; then
DATE=$(git show -s --format=%ci $hash)
DATE=${DATE:0:10}
echo $DATE
git show $hash:script.php > $SCRIPTDIR/$DATE.php
fi
done
Al final de esto tendremos un directorio con todos los script con su correspondiente fecha listo para usarse. Pero como siempre nos encontraremos con otro problema, y es que la ejecución es muy lenta. Analizando el algoritmo de los script php vemos que hay un bucle con 10 millones de iteraciones que es el responsable de la lentitud:
$counter = $secret3;
for ($i=0; $i < 10000000; $i++) {
# This loop makes the passwords hard to reverse
$counter = ($counter * $secret1) % $secret2;
}
Vemos que el valor de $counter en cada iteración se vuelve a multiplicar por $secret1 y se calcula el módulo una y otra vez. Es un caso de exponenciación modular muy utilizada en criptografía, y de la cual existe un cálculo rápido implementada en la mayoría de los lenguajes. Así que el bucle con 10 millones de iteraciones se puede sustituir por la siguiente veloz sentencia:
$counter = ($secret3 * bcpowmod($secret1, 10000000, $secret2)) % $secret2
Esto mejora de forma considerable los tiempos de cálculo pero existen ejemplos que tardan mas. Por lo que la última opción es extraer los valores $secret1 y $secret2 que es lo que cambia cada día y re-implementar el algoritmo en otro lenguaje para obtener un mejor rendimiento y así evitar tantas llamadas a lenguajes interpretados, ademas de poder precalcular algunas operaciones.
11. Colors
De nuevo un problema de grafos. Debemos calcular el tiempo mínimo para llegar a cada una de las distintas galaxias que están conectadas por agujeros de gusano, que sólo podremos utilizar si poseemos la energía de color adecuada.
Inicialmente parecía claro tener que aplicar Bellman–Ford para obtener todos los caminos mínimos, pero en este problema las aristas pueden estar activas o no en función de nuestro estado, e incluso existir bucles (como ir y volver a otra galaxia para conseguir energía de otro color para poder usar un tipo de agujero de gusano).
Así que opté por implementar el algoritmo de búsqueda manualmente, aunque no es la solución válida ya que el tiempo crece exponencialmente. Del enunciado se intuye que nuestro estado y cada galaxia se podría representar como un número binario, donde cada bit indica la existencia o no de la energía de un color, y las aristas como máscaras binarias para saber si la cumplimos o no. Aunque en mi caso no exploré esta opción y decidí saltar el ejercicio por que el tiempo se terminaba.
12. That’s a lot of moneyz
Este ha sido mi otro problema favorito del concurso de este año. Tenemos que ayudar a nuestro amigo a contar monedas. Para ello, al conectarnos a la dirección y el puerto indicados, se nos envían una serie de imágenes JPEG de las monedas que tenemos contar (siempre imágenes distintas). Si nos conectamos con telnet o netcat veríamos esto:

Si procesamos los datos adecuadamente veríamos imágenes como esta:

Las imágenes vienen dañadas, con algunas secciones verticales invertidas, pero son fácilmente corregibles ya que cada dos columnas de 40 pixeles se invierte la imagen. Inicialmente intenté resolverlo analizando el histograma de las imágenes, para intentar averiguar las monedas contando la cantidad de determinados colores que existen, pero al ser JPEG existía mucho ruido y zonas difuminadas.
Así que toca echar mano de procesamiento de imágenes, cosa que siempre me había llamado la atención pero que nunca había trasteado. Para solucionarlo utilicé el que parece la librería mas popular: OpenCV y su binding para Java.
Una vez restaurada la imagen, el primer paso sería detectar los distintos círculos que existen en la imagen que corresponderían con las monedas aplicando CHT (Circle_Hough_Transform). Aplicado sobre la imagen, obtenemos una lista de puntos que se corresponden con los centros de las circunferencias detectadas junto con sus radios.
Como cada moneda tiene un tamaño distinto, quizás podríamos saber de qué moneda se trata sabiendo el radio mas próximo. Desgraciadamente las detecciones no tienen tal nivel de exactitud, y a veces detecta círculos mas pequeños o ligeramente desplazados debido a la calidad de las imágenes.
Después de distintos intentos, opté por utilizar el algoritmo Template Matching, que permite buscar zonas de imágenes similares. Así que puesto que detectaba correctamente los centros de las monedas, lo que hice fue extraer una región cuadrada de cada uno de los centros detectados. Por otro lado, generé pequeños cuadrados de los centros de cada una de las monedas posibles que los usuarios como los patrones a buscar:

Por último, para cada sección cuadrada realicé una búsqueda de los patrones de las monedas para ver si se encontraba y por tanto saber de qué moneda se trataban.

Desgraciadamente para mi lo resolví minutos después de que se cerrara el tiempo límite y no pude entregar la solución. Para que os hagáis una idea de cómo les gusta a los de Tuenti complicar las pruebas, esta era una de las últimas imágenes que teníamos que resolver:
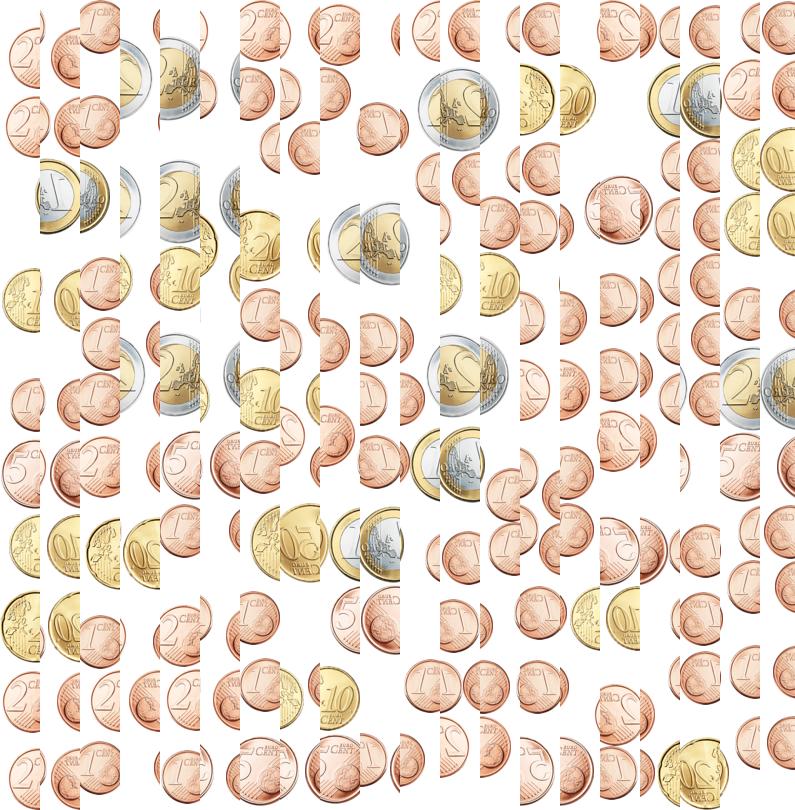
13. R’lyeh
Después de una intrigante introducción basada en Lovecraft, se nos insta a averiguar la relación entre los números esculpidos y escritos sobre una estatua. Tenemos la función que dado un número esculpido, nos devuelve el número escrito correspondiente. Pero se nos pide justo lo contrario, dado un conjunto de número escritos, averiguar el esculpido correspondiente. El problema es tan sencillo como implementar la función inversa a la que no dan. Sencillo si no fuera por el aspecto de esta función:
int64_t carvedToWritten(int64_t n)
{
int64_t r = 0;
for (int64_t i = 0; i < 64; ++i)
{
int64_t a = 0;
for (int64_t j = n; j >= 0; --j)
{
int64_t b = 0;
for (int64_t k = 0; k <= i; ++k)
{
int64_t c = a ^ ((i & (n ^ j) & 1) << k);
a ^= (j & (1LL << k)) ^ b;
b = (((c & j) | ((c ^ j) & b)) & (1LL << k)) << 1;
}
}
r |= (a & (1LL << i));
}
return r;
}
Misión imposible intentar entender que hace. Si usamos esta función para generar 1000 pares de números (carved - written) y los ordenamos por written tampoco apreciamos relación alguna:
written | carved written | carved
--------+------- --------+-------
1 | 1 24 | 143
2 | 4 25 | 17
4 | 8 30 | 19
5 | 9 32 | 64
6 | 3 33 | 66
7 | 5 34 | 587
8 | 16 37 | 73
9 | 18 64 | 128
14 | 572 65 | 129
16 | 32 66 | 11
17 | 33 67 | 14
18 | 36 70 | 12
20 | 7 71 | 38
21 | 10 72 | 144
23 | 6 75 | 573
...
Si nos fijamos bien en la función, vemos que hay un bucle exterior que itera 64 veces y realiza la operación r |= (a & (1LL << i)). Que es lo mismo que establecer los bits del 0 al 64 del resultado final. Si agregamos un printf en este punto para ver los valores que va tomando la variable a en cada iteración observamos lo siguiente:
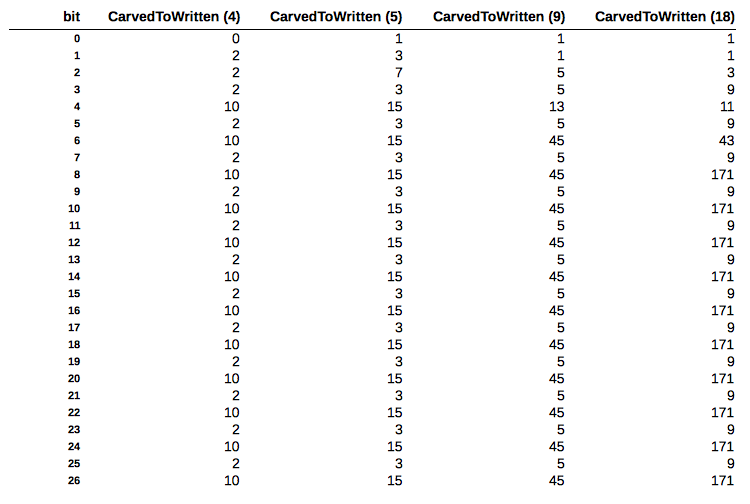
Ahora si que vemos un patrón que se repite constamente. Para los bits impares se toma el valor (n + 1) / 2, y para los pares n * (n + 1) / 2. Así que podemos simplificar la función original, que además mejorará el rendimiento:
int64_t carvedToWrittenFast(int64_t n)
{
int64_t r = 0;
for (int64_t i = 0; i < 64; ++i)
{
int64_t a = 0;
if (i % 2 == 0) {
a = n * (n + 1) / 2;
} else {
a = (n + 1) / 2;
}
r |= (a & (1LL << i));
}
return r;
}
Una vez comprobamos que esta nueva función es equivalente a la primera, podemos analizar su funcionamiento. Podemos obtener los bits impares de n directamente del valor de r, realizando la operación inversa a (n + 1) / 2:
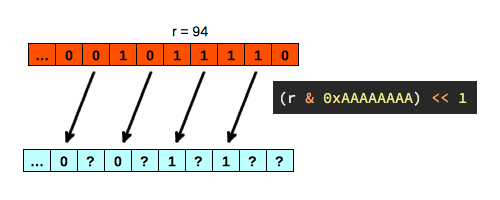
Como sabemos que el número objetivo es de 32 bits, y gracias a la operación anterior conocemos ya 16 bits del valor final, la opción mas sencilla es calcular por fuerza bruta los otros 16 bits restantes, lo que nos llevará a probar 65536 valores en el peor de los casos:
uint32_t writtenToCarved(int64_t r) {
uint32_t m = (r & 0xAAAAAAAA) << 1;
for (int i = 0; i < 0xFFFF; i++) {
uint32_t n = m;
for (int k = 0; k < 16; k++) {
n |= (i & (1 << k)) << (k + 1);
}
if (carvedToWrittenFast(n - 1) == r) {
return n - 1;
} else if (carvedToWrittenFast(n) == r) {
return n;
}
}
return 0;
}
Me quedan por solucionar dos problemas: Blackjack y Intervals, que en otro momento intentaré solucionar y actualizaré esta entrada con su correspondiente análisis.